|
文章题目:应用“数形结合”思想培养学生创新能力
内容提要:
“数形结合”思想是重要的数学思想之一,本文从一个奇妙的数学问题引入,提出在小学数学的教学中,应用“数形结合”的思想进行教学,可以使形象思维和逻辑思维有机的结合,培养学生的创新能力。并从三个方面,简要论述作者在教学中的做法。
摘要:
“数形结合”思想是重要的数学思想之一,本文从一个奇妙的数学问题引入,提出在小学数学的教学中,应用“数形结合”的思想进行教学,可以使形象思维和逻辑思维有机的结合,培养学生的创新能力。并从三个方面,简要论述作者在教学中的做法。
关键词:数形结合 创新能力
正文:
一、 从一个奇妙的数学问题谈起
一位魔术师拿着一块边长为13分米的正方形地毯,对朋友说:“请您把这块地毯分成四小块,再把它们缝成一块长21分米、宽8分米的长方形地毯。”
既然是魔术,说明这种现象或者是必然规律,或者是视觉误差。对于这个问题,一个小学生都可以通过计算得出,这是不可能的。边长时13分米的正方形的面积:13×13=169(平方分米);长为21分米,宽为8分米的长方形的面积:21×8=168(平方分米);魔术师说的情况到底能不能发生呢?如图所示:
图1

图2
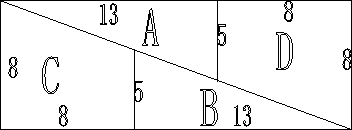
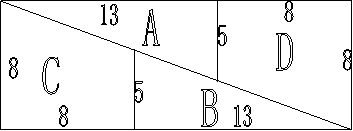 第一次看这个图,感觉很奇妙,明明只是分解后重新组合,为什么重新组合后面积就发生变化了呢?通过看图却不能发现问题出在哪里。但自己又深深地知道,面积是不可能发生变化的。这个图是利用了我们视觉上的误差,通过计算就可以找到原因。图3 第一次看这个图,感觉很奇妙,明明只是分解后重新组合,为什么重新组合后面积就发生变化了呢?通过看图却不能发现问题出在哪里。但自己又深深地知道,面积是不可能发生变化的。这个图是利用了我们视觉上的误差,通过计算就可以找到原因。图3
解:假设虚线的长度为X。
则
也就是说在对角线中段附近有微小的重叠。正是由于对角线的这点儿叠合,而导致了丢失了1平方分米的面积。
虽然问题的答案已经找到,但我还是觉得这个问题很奇妙。是不是任意一个正方形分成四部分后都会有这种情况呢?通过实验验证,答案是否定的。这种情况并不是必然出现的。这就说明,这种情况的出现,与相关数据是有着密切关系的。
意大利数学家斐波那契(Fibonacci,1170——1250)在研究数学的过程中发现一个数列。人们为纪念斐波那契的发现,在这个数列前面增加一项“1”后得到数列:
1,1,2,3,5,8,13,21,34,55,89,……叫做“斐波那契数列”,这个数列的任意一项都叫做“斐波那契数”。斐波那契数列有一个有趣而重要的性质: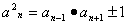 (n≥2) (n≥2)
通过斐波那契数列,我们可以知道,这种奇妙的问题还可以构造出很多,只要把上题中的长方形长、正方形边长和长方形的宽,换成连续的三个斐波那契数就可以了。正是这些特殊的数,使图形发生了这样奇妙的现象。
从上面这个奇妙的数学问题不难看出,图形出现的奇妙现象与数有着非常紧密地联系,数的特点决定了图形的特点,图形的特点体现着数的特点,“数”与“形”的完美结合,创造出了奇妙的现象。“数形结合”思想是重要的数学思想之一,在小学数学的教学中,应用“数形结合”的思想进行教学,可以使形象思维和逻辑思维有机的结合,培养学生的创新能力。
二、 “数”与“形”
1、 数学研究的内容
数学是研究空间形式和数量关系的科学。数与形式数学中最基本、最原始的概念。从数的概念出发发展出了算数、代数以及庞大的分析系统。从形的概念出发,发展出欧氏几何、非欧几何,直到现在的流形理论。数和形这两个概念在数学的发展过程中,互相影响,交互作用。1637年卡笛儿的著作中给出了字母符号的代数和解析几何原理,这就是引进坐标系和利用坐标方法把具有两个未知数的任意代数方程看成平面上的一条曲线。解析几何的主要作用:
1) 通过计算来解决作图问题;
2) 求由某种几何性质给定的曲线的方程;
3) 利用代数方法证明新的几何定理;
4) 反过来,从几何方面来看代数方程。
因此,解析几何是一门把代数和几何知识结合起来研究的学科。
2、 “数”与“形”的关系
数形结合,就是根据数学问题的条件和结论之间的内在联系分析其代数含义,又揭示其几何直观,使数量关系与空间形式和谐地结合起来。数形结合思想,就是将抽象的数学语言与直观的图形结合起来,使抽象思维与形象思维结合。通过对图形的认识、数形转化,以提高思维的灵活性、形象性、直观性使问题化难为易,化抽象为具体。
把数与形结合在一起思考、分析、研究,是学习数学常用的思想方法。有机的把数和形相结合是学习数学的好方法,也是解决问题的好方法。在小学数学的教学中,为了让学生对所学的知识有更深刻的理解,经常采用“数形结合”的方法,提高学生对数学本身的感悟与理解。
3、 “数”与“形”与创新能力培养
培养学生的创新能力是教学的一个重要任务。根据脑科学理论,创新能力是个人多种心理品质和能力的复杂的、高水平的结合。创新能力不是凭空产生的,它是以扎实的知识和一般能力为基础,是从一般能力发展而来。就是说,创新能力的培养是和不同领域的学科知识及有关能力相联系的,创新能力应该从小培养。
创新活动的核心是创造性思维。什么是创造性思维呢?我们认为:创造性思维是创造过程中的思维活动,它主要是两种思维(抽象思维和形象思维)新颖的灵活的有机的结合。
数与形的结合,与脑科学理论相吻合。“数”更多的是发展逻辑思维,而“形”更多的是发展形象思维。“数”与“形”结合,相互渗透,把代数式的精确刻画与几何图形的直观描述相结合,使代数问题、几何问题相互转化,使抽象思维和形象思维有机结合。应用“数形结合”思想,就是充分考查数学问题的条件和结论之间的内在联系,既分析其代数意义又揭示其几何意义,将数量关系和空间形式巧妙结合,来寻找解题思路,使问题得到解决。 因此,数形结合的过程是两种思维相结合的过程,是培养学生的创新能力的过程。
三、 小学数学教学中运用“数形结合”思想,培养学生创新能力。
1、通过“线段图”表示数量之间的关系,运用“数形结合”,培养创新能力。
线段图是小学生学习应用题的重要辅助工具。它可以形象地、具体地反映应用题的数量关系,启发学生的解题思路,帮助学生找到解题的方法。
应用题是小学生学习的一个难点。小学生初学文字叙述的简单应用题的时候,因为文字题比较抽象,所以学生往往分不清题目中的已知条件和问题,特别是条件和条件、条件和问题的相互关系,不少学生搞不清楚。低年级小学生知识少,接受能力差,理解题意和选择算法都比较困难。为了减少学生学习应用题的困难,教学中,通过线段图来表示应用题中的各个数量,以线段的长短表示数量的大小,以线段的位置、长短、对应表示数量关系。这样就把应用题中比较抽象的数量关系用线段图把它形象地描绘出来了。学生通过看图、画图,对应用题中的内容和各个具体内容之间的关系就看得清楚了。在学习分数应用题时,如果不画线段图,学生是很难理解的。
图4(红花比黄花多10朵)
图5
(商店运来茄子比西红柿的多4千克,西红柿比茄子多20千克,商店运来茄子多少千克?)
对于含有复杂数量关系的复合应用题、分数应用题、百分数应用题、比例应用题,如果能够熟练地画出线段图,就可以把较复杂的数量关系较为明显地表示出来,就能帮助学生较快找到解题方法,列出算式,求出正确的答案。尤其是对学生解答分数乘、除法应用题,画线段图更能起到有益的辅导作用。实践证明,运用线段图来教学应用题,不仅可以减少学生学习中的困难,增强学习应用题的兴趣,而且能进一步调动学生思维的积极性,提高学生分析应用题和解答应用题的能力。教学中线段图的运用,使数量关系与其紧密结合,体现了“数形结合”的思想。同时,发展了学生的形象思维,使两种思维紧密相结合,培养学生的创新能力。
2、借助长方体展开图来计算表面积,运用“数形结合”,培养创新能力。
长方体的表面积就是长方体六个面的面积之和,根据长方体的特点,对面的面积相等,总结出长方体表面积的公式。在教学长方体表面积这一内容时,为了更深刻的理解表面积的概念和掌握求长方体表面积的方法采用了下面的方法。首先,画出长方体的立体图形,标出长、宽、高。(图5)其次,画出长方体的展开图,标出相关数据。(图6)最后,边列式边在展开图中相应的长方形上画上阴影。(图7)

图6
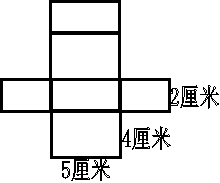 图7 图7
图8

a) b) c)
a)5×4×2 b)5×4×2+4×2×2 c)5×4×2+4×2
×2+5×2×2
通过这样的方法,可以使学生更深刻地理解表面的概念,对于灵活解决表面积的问题很有帮助。另外,通过图形和算式的结合,可以避免重复和遗漏六个面,正确的计算长方体的表面积。借助长方体的展开图来理解表面积的概念,来帮助计算长方体的表面积,使计算与图形紧密结合,体现了“数形结合”的思想。在发展形象思维的同时,使两种思维紧密相结合,培养学生的创新能力。
3、借助图形特点来分析问题,运用“数形结合”,培养创新能力。
有一些特殊的应用题可以借助图形的特点来分析解答,使数量关系和图形很好的结合,最终解决实际问题。实验教材第六册(P127)有这样一道应用题。亮亮家离学校55米,芳芳家离学校45米。亮亮家与芳芳家相距多少米?这是一道分情况讨论的题目,对于小学生有一定的难度。在分析、解答这道题的时候,就可以借助图形的特点来分析、理解。
通过“亮亮家离学校55米”可以知道,亮亮家在以学校为圆心,以55米为半径的圆上。同理,芳芳家在以学校为圆心,以45米为半径的圆上。(如图8所示)
如果亮亮家、芳芳家和学校在同一条支线上:
 (1)亮亮家和芳芳家在学校同侧(图9(a)) (1)亮亮家和芳芳家在学校同侧(图9(a))
55-45=10(米)
(2)亮亮家和芳芳家在学校两侧(图9(b))
55+45=90(米)
如果亮亮家、芳芳家和学校不在同一条支线上:(图9(c))

亮亮家与芳芳家的距离
比10米多,比100米少。
通过利用圆的特点,分析解决了这样一个不是很容易说情的问题。体现了“数形结合”的优势,使复杂的问题简单化,形象直观地解决实际问题。借助图形的特点来解决实际问题,更直接的体现了“数形结合”思想的优越性。可见,把形象思维与逻辑思维紧密地结合,可以培养学生的创新能力。
在数学研究中,数是形的抽象概括,形是数的直观表现。数与形的结合,一方面是通过数量关系的讨论来研究几何图形的性质,另一方面是利用几何图形的直观,揭示数量关系许多深刻的特性。“数形结合”的思想方法,是研究数学问题的一个基本方法,深刻理解这一观点,有利于提高我们发现问题、分析问题和解决问题的能力。在教学中,应该更多地运用“数形结合”的思想,发展了形象思维,培养学生的创新能力。
参考文献
马芯兰《小学数学能力的培养与实践》 山东教育出版社 1999
温寒江 连瑞庆《构建中小学创新教育体系》北京科技出版社 2002
张顺燕 《数学的源与流》 高等教育出版社 2000
单位:北京市朝阳区实验小学
姓名:王晓松
通讯地址:北京市朝阳区工体北路幸福一村四巷36号
邮编:100027
电话:13911050582
|

